Mathematics
The integration of mathematics in our cochlear implant project optimizes signal processing, power management, and system performance through algorithms such as FFT, filtering, and gain control. Mathematical modeling ensures the device delivers high-quality auditory results while efficiently utilizing power and resources.
Integration
Automatic Gain Control (AGC)
Gain control uses logarithmic functions to adjust the amplification based on signal strength, ensuring signals remain within a usable dynamic range.
Signal Processing
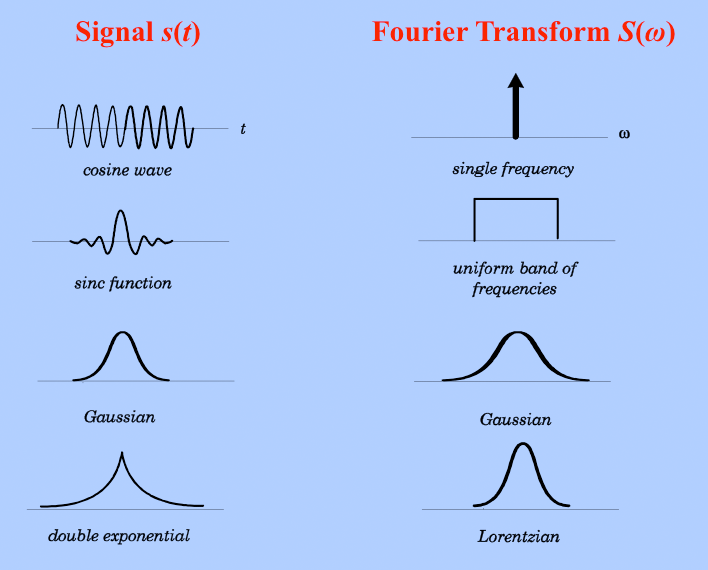
Fast Fourier Transform (FFT) is used to convert time-domain signals (audio) into frequency-domain signals for analysis.
Automatic Gain Control (AGC)
-
Concept: The AGC mechanism adjusts the input audio signal’s amplitude to maintain a consistent volume level for the user. This is crucial because sound levels in the environment can vary widely, and the implant must ensure the signals remain within a comfortable and usable range.
-
Mathematical Principle: AGC involves calculating the gain factor based on the input signal amplitude and the desired output signal level. The gain is dynamically adjusted using the following formula:
G= Atarget
Ainput
-
where:
-
G = gain factor,
-
Atarget = target amplitude,
-
Ainput = measured amplitude of the input signal.
-
Signal Processing (Fourier Transform and Filtering)
-
Concept: Signal processing converts raw sound signals into a digital format that the cochlear implant can process. It involves filtering, frequency analysis, and reconstruction of the sound signals.
-
Mathematical Principle: The Fourier Transform is used to break down complex audio signals into their constituent frequencies. The Discrete Fourier Transform (DFT) is particularly important in digital signal processing:
-
X(k)=∑n=0N−1x(n)e−j2πknN
-
where:
-
X(k) = frequency domain representation,
-
x(n) = time domain signal,
-
N = total number of samples,
-
k = frequency index,
-
j = imaginary unit (j^2=−1)